INTERVALO DE CONFIANZA PARA LA DIFERENCIA DE DOS MEDIAS.
Sean X11, X12, … X1n1, una muestra aleatoria de n1 observaciones tomadas de una primera población con valor esperado µ1 y varianza s
1, y X21, X22, … X2n2 una muestra aleatoria de n2 observaciones tomada de la segunda población con valor esperado µ2 y varianza s
Si son las medias muestrales, la estadística es un estimador puntual de µ1 - µ2, y tiene una distribución normal si las dos poblaciones son normales, o aproximadamente normal si
cumple con las condiciones del teorema del limite central (tamaños de muestras relativamente grandes). Es decir, . Por lo tanto,
Para calcular el intervalo de confianza para la diferencia de dos medias se debe saber si las varianzas poblacionales son conocidas o desconocidas, y en caso de que sean desconocidas, se debe probar si son iguales o diferentes. Cada uno de estos tres casos se analizarán por separado
Varianzas conocidas
Si las varianzas poblacionales son conocidas, los pasos a seguir para encontrar el intervalo de confianza son los siguientes:
a) El estadístico usado como estimador puntual de la diferencia de medias µ1 - µ2 será T = , que es un estimador suficiente b) La variable aleatoria asociada con el estimador será la variable normal estándar dada por:
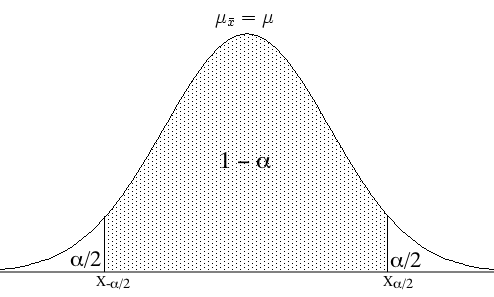
c) Para calcular el intervalo de confianza se debe tener en cuenta la siguiente probabilidad:
Manipulando la expresión anterior en forma similar a como se hizo en los casos de una sola muestra se llega al siguiente teorema que nos define el intervalo de confianza para la diferencia entre dos medias µ1 - µ2 con varianzas conocidas s
1 y s
2.
Teorema. Si son las medias de dos muestras aleatorias independientes de tamaño n1 y n2 tomadas de poblaciones que tienen varianzas conocidas s
1 y s
2, respectivamente, entonces un intervalo de confianza del 100(1-a)% para µ1 - µ2 es:
Ejemplo. Construya un intervalo de confianza del 94% para la diferencia real entre las duraciones de dos marcas de bombillos, si una muestra de 40 bombillos tomada al azar de la primera marca dio una duración media de 418 horas, y una muestra de 50 bombillos de otra marca dieron una duración media de 402 horas. Las desviaciones estándares de las dos poblaciones son 26 horas y 22 horas, respectivamente.
Solución. Tenemos que:, , s1 = 26, s2 = 22, n1 = 40, n2 = 50, Z0.03 = 1.88. El intervalo de confianza es, entonces:
El hecho de que ambos límites sean positivos, y por lo tanto no contengan el valor cero indican que ambas marcas no tienen la misma duración media, y sugiere que pueda pensarse que la primera marca de bombillos tenga una duración media superior a la segunda.
jueves, 15 de abril de 2010
Suscribirse a:
Enviar comentarios (Atom)






No hay comentarios:
Publicar un comentario